요즘은 C/C++보다 Rust로 알고리즘 문제를 풀고 있어서 문제마다 필요한 라이브러리를 공부 중이다.
C++이나 Java는 구글링하면 PS에 필요한 라이브러리 사용법 포스팅이 많은데 Rust는 국내에 없어서 쓴다.
물론 공식 문서가 있지만 영어가 불편한 분들을 위해 필요한 것만 한글로 알잘딱깔센으로 써보겠다.
내부 구현이나 철학은 필요없고, 라이브러리 사용법만 알고 싶다면 카테고리에서 바로 넘어가면 된다.
그렇지만 내부 구현이나 동작 흐름 위주로 분석한 글이라는 점을 참고하자.
그래서 skip 하지 않고 이 글을 다 읽으면
- 우선순위 큐 자료구조와 힙/힙 트리
- Rust BinaryHeap의 내부 구조와 동작 흐름
- C/C++, Java와 비교했을 때의 차이점
은 확실히 이해할 수 있을 것이라 장담한다.
📖 BinaryHeap 개념
BinaryHeap은 자료구조(ADT) 관점으로 보면 우선순위 큐 (Priority Queue)다.
일반적으로 내부는 힙(heap)으로 구현하고, 형태에 따라서 최대 힙이나 최소 힙이 될 수 있다.
※ 우선순위 큐(Priority Queue): 삽입된 원소들 중 우선순위가 가장 높은 원소를 빠르게 조회/제거하기 위한 자료구조
힙(heap) / 힙 트리(heap tree)
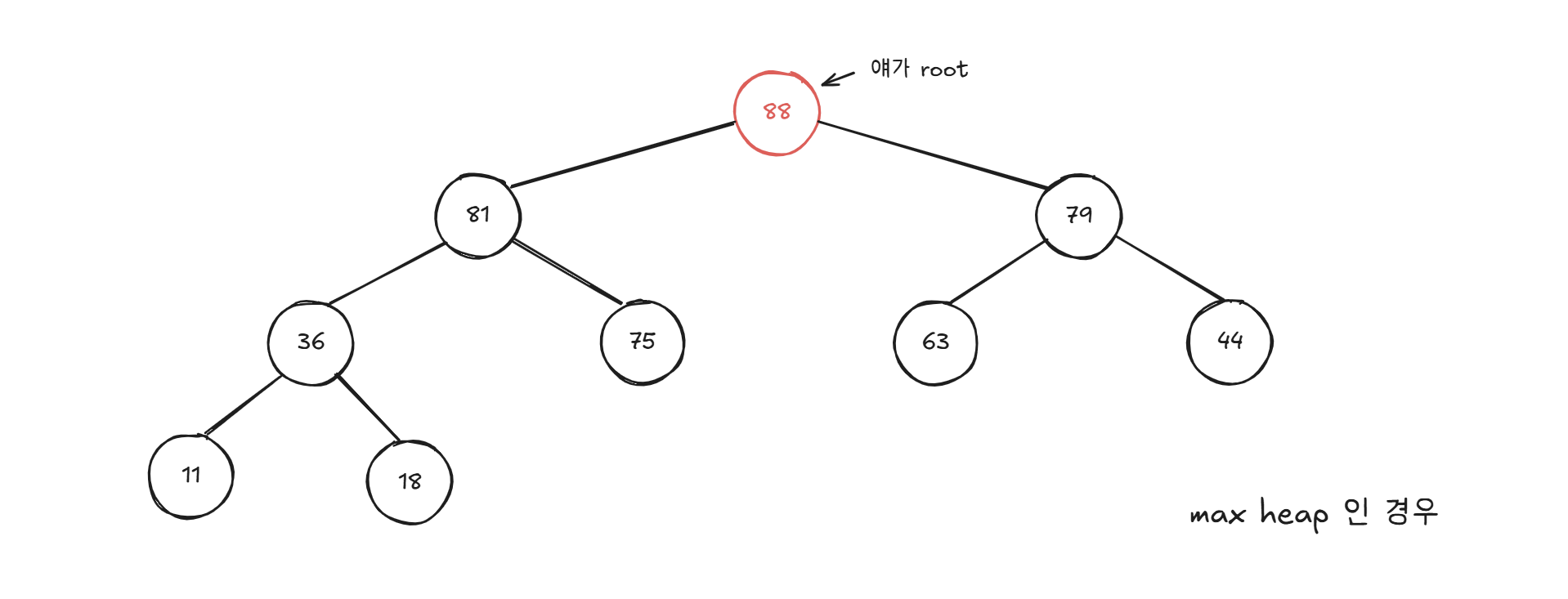
이해하기 쉽게 그려봤는데, 힙 트리는 완전 이진 트리(complete binary tree) 구조를 가진다.
그렇다고 힙을 완전 이진 트리 구조로만 구현해야하는 건 아닌데, 삽입/삭제 효율을 위해서 사용한다.
그림에서 볼 수 있듯 우선 순위가 가장 높은 원소가 root에 있어서 O(1)에 접근 가능하다.
최상단인 root가 중요하지 나머지 원소들은 정렬이 되어있지도 않고, 중요치 않다.
내부 구현에서 새 원소 추가/제거 시, 부모-자식을 비교하면서 위치를 재조정하기 때문이다.
최대 힙(Max-Heap)은 부모가 자식보다 큰 구조로, root에 가장 큰 값이 위치한다.
반대로 최소 힙(Min-Heap)은 부모가 자식보다 작고, root에 가장 작은 값이 위치한다.
다시 말하지만, 정렬된 구조는 아니고 부모-자식 관계만 성립할 뿐이다.
[다른 언어와 비교] C/C++과 Java에서의 우선순위 큐 🔍
다른 언어와 비교는 하나도 안 궁금하고, Rust만 알고 싶으면 건너뛰어도 된다.
그래도 이걸 읽으면 다른 언어들과 다른 Rust의 철학을 확실하게 느낄 수 있다.
아무래도 알고리즘 풀이에는 C/C++을 사용하고,
백엔드 개발엔 Java를 사용하다보니 언어를 배울 때 비교하는 방식으로 공부하니 좋았다.
언어마다 철학도 다르고, 구현도 다르니 마지막엔 각각의 장단점도 비교해서 종합해보자.
1) C언어 → 표준 라이브러리 없고, 직접 구현해야 함
C에서는 우선순위 큐가 라이브러리 형태로 제공되지 않아서 직접 힙을 구현해야 한다.
어렵지는 않고 그냥 위의 부모-자식 간 규칙을 그대로 배열에 적용하면 된다.
매번 필요할 때마다 직접 구현해야하니 귀찮다는 단점이 있지만, 추상화가 적고 성능도 빠르다.
최대 힙으로 우선순위 큐 직접 구현한 코드
#include <stdio.h>
int heap[100001];
int pos = 1;
void swap(int* x, int* y){
int tmp = *x;
*x = *y;
*y = tmp;
}
void insert(int val){
int idx = pos;
heap[pos++] = val;
// 부모보다 크면 위치 교환 반복.
while ((idx > 1) && (heap[idx >> 1] < heap[idx])) {
swap(&heap[idx], &heap[idx >> 1]);
idx >>= 1;
}
}
int delete(){
if (pos == 1) return 0;
int top = 1, ret = heap[1];
// 가장 마지막 원소를 루트로 올림.
heap[top] = heap[--pos];
heap[pos] = 0;
while ((top << 1) < pos) {
int child = top << 1;
// 두 자식 중 더 큰 애로 타겟.
if (child + 1 < pos && heap[child + 1] > heap[child]) child++;
if (heap[child] > heap[top]) {
swap(&heap[top], &heap[child]);
top = child;
}
else break;
}
return ret;
}
2) C++ → std::priority_queue
표준 라이브러리로 priority_queue가 제공돼서 이걸 쓰면 간편하다.
priority_queue<T, Container, Compare>위와 형태인데 내부 컨테이너로는 vector가 사용되고, 내부 구현 역시 마찬가지로 이진 힙 방식이다.
comparator는 컴파일 타임에 고정되고, 별도로 설정하지 않으면 최대 힙으로 동작하는 게 default다.
컴파일 타임에 고정되기 때문에 비교 자체를 아예 코드로 직접 박아둘 수 있게된다.
그렇기 때문에 priority_queue<int, vector<int>, less<int>>와
priority_queue<int, vector<int>, greater<int>>는 아예 다른 타입이라고 보면 된다.
👉 즉, 생성 이후 기준을 바꿀 수 없다는 제약이 있지만 오버헤드가 없어 성능이 좋다 (유연성 x 성능 o)
#include <iostream>
#include <queue>
#include <vector>
#include <functional> // 비교 함수 greater(최소힙), less(최대힙) 사용에 필요함
using namespace std;
int main() {
priority_queue<int> pq; // 기본 형태: priority_queue<int, vector<int>, less<int>> pq;
int values[] = {8, 7, 30, 11, 9};
for (int v : values) {
pq.push(v);
}
cout << "현재 원소 개수: " << pq.size() << '\n';
while (pq.size() > 0) {
int top = pq.top();
pq.pop();
cout << top << '\n';
}
}
3) Java -> java.util.PriorityQueue
Java에서도 PriorityQueue를 제공하는데, 특이한 점으로는 기본이 최소 힙이라는 것이다.
모든 원소가 객체이고, Comparator도 인터페이스로 런타임에 전달되는 객체다.
그래서 실행 중에 조건에 따라 기준을 다르게 설정할 수 있게 된다.
다만 Comparator 객체를 참조하고 compare() 메서드를 호출해야 한다는 점에서 오버헤드가 발생한다.
👉 즉, C++과는 반대로 성능을 일부 포기하고 유연성을 챙겼다고 보면 된다.
import java.util.PriorityQueue;
import java.util.Comparator; // 최대 힙 변경 시 사용
public class Main {
public static void main(String[] args) {
PriorityQueue<Integer> heap = new PriorityQueue<>();
// 최대 힙: PriorityQueue<Integer> heap = new PriorityQueue<>(Comparator.reverseOrder());
int[] values = {8, 7, 30, 18, 90};
for (int v : values) {
heap.offer(v);
}
System.out.println("현재 원소 개수: " + heap.size());
while (!heap.isEmpty()) {
Integer top = heap.poll();
System.out.println(top);
}
}
}
📝 각 언어별 우선순위 큐 3줄 요약
1. C는 성능을 위해 모든 걸 직접 구현하도록 맡겼고,
2. C++은 비교를 컴파일 타임에 고정해서 성능을 챙겼고,
3. Java는 일부 오버헤드를 감수하고 런타임 유연성을 챙겼다.
Rust의 우선순위 큐는 이들과 뭐가 어떻게 다른가?
C++과 Java는 모두 정렬 기준인 Comparator를 외부에서 주입하는 방식을 사용했다.
It is a logic error for an item to be modified in such a way that the item’s ordering relative to any other item, as determined by the Ord trait, changes while it is in the heap.
하지만 Rust는 정렬 순서가 힙이 소유해야 할 특성이 아니라 값 자체의 성질이라고 본다는 관점을 드러낸다.
BinaryHeap은 Ord를 호출할 뿐 비교 기준에 대해 알지 못 하고, 값이 제공하는 비교 결과를 소비한다.
따라서 힙 내부 원소의 Ord 기준 상대적 순서를 바뀌도록 수정하는 행위는 logic error로 분류한다.
👉 즉, 비교 정책에 대한 책임을 힙에서 분리했다고 볼 수 있다.
근데 힙에서 비교 정책 책임을 분리하는 게 왜 필요한지 모르겠는데요?
앞서 살펴봤던 것처럼 C++과 Java에서는 성능과 유연성 사이에서 줄다리기를 했었다.
그런 것도 아니고 책임 분리가 C/C++, Java에서 발생하던 문제를 막는 것도 아니다.
예를 들어 힙 내부 원소의 값을 변경하면 C/C++, Java, Rust 모두 문제가 터진다.
그럼 비교 정책을 힙이 들고 있고 없고의 책임 문제는 뭐가 중요했던 걸까?
더 나아가서 C/C++, Java와 비교해서 Rust의 방식은 뭐가 어떤 점에서 어떻게 다른 걸까?
🎁 책임 분리로 얻는 이득
일단 설명 전에 두 가지 팩트를 짚고 넘어가자.
팩트 1. 우선순위 큐에서 중요한 건 힙의 불변성(부모 노드가 자식 노드보다 우선순위가 높다)이다.
팩트 2. 힙 내부 원소 값이 변경되서 순서가 깨지는 건 어떤 언어든 완전히 막기 어렵다.
Q. 근데 2는 힙 내부 값을 불변으로 구성하면 될 것 같은데 왜 안 했을까? 🤔
내부 원소가 불변이면 Ord 의미가 바뀌는 문제 자체가 발생하지 않게 될텐데?
A. 나름대로의 조사결과: BinaryHeap엔 peek_mut()같은 메서드도 존재한다.
Rust에서는 이런 사용을 막기보다는 Ord에 영향을 주면 logic error라고 규정한 걸로 보인다.
비교 정책을 우선순위 큐가 소유하는 C++과 Java의 경우 힙 불변성이 깨졌을 때 원인을 좁히기 어렵다.
- 힙 연산 구현 자체 버그인지
- Comparator 구현 문제인지
- Comparator가 참조하는 외부 상태 변화 탓인지
3번(비교 정책이 참조하는 외부 상태 변화) 예시
int threshold = 10;
struct Cmp {
bool operator()(int a, int b) const {
// threshold라는 외부 상태에 의존
if (a >= threshold && b < threshold) return false;
if (a < threshold && b >= threshold) return true;
return a < b;
}
};
priority_queue<int, vector<int>, Cmp> pq;
pq.push(5);
pq.push(20);
// 여기까지는 threshold = 10 기준으로 힙이 만들어짐
threshold = 100; // 힙 연산 없이 기준이 바뀜
반면에 Rust의 BinaryHeap은 값이 제공하는 Ord 결과만을 소비하는 방식이라,
비교 정책이 힙의 책임이 아니기 때문에 원인을 값 자체의 Ord 위반으로 한정할 수 있게 된다.
👉 힙 불변성이 깨져도 힙 구현의 문제가 아니라 값이 Ord를 위반한 결과임을 알 수 있다.
즉, Rust의 방식은 C++, Java에서 못 막는 문제를 해결했다!가 아니라
문제가 생겼을 때 그 책임이 어디있는지 명확히 드러내려 한 것이다.
성능이나 기능의 차이라기보다 설계 철학의 차이라고 볼 수 있다.
🛠️ Rust의 std::collections::BinaryHeap
A priority queue implemented with a binary heap.
This will be a max-heap.
공식문서에서는 아주 깔끔하게 이진 힙으로 구현된 우선순위 큐고, 최대 힙이라고 소개하고 있다.
BinaryHeap 내부 구조
내부 구조를 보면 C++과 마찬가지로 vector 기반으로 돌아가는 것을 알 수 있다.
#[stable(feature = "rust1", since = "1.0.0")]
#[cfg_attr(not(test), rustc_diagnostic_item = "BinaryHeap")]
pub struct BinaryHeap<
T,
#[unstable(feature = "allocator_api", issue = "32838")] A: Allocator = Global,
> {
data: Vec<T, A>,
}
구조적으로는 완전 이진 트리를 배열(Vec)로 표현하는 전형적인 방식이다.
- 부모 인덱스: (i - 1) / 2
- 왼쪽 자식 인덱스: 2 * i + 1
- 오른쪽 자식 인덱스: 2 * i + 2
각 노드는 인덱스 계산으로 부모/자식에 접근한다.
힙을 직접 구현해봤다면 익숙한 그 구조다.
힙 불변성 유지 핵심 메커니즘 ⭐
중요해서 반복해서 말하는데, 우선순위 큐에서 가장 중요한 건 힙 불변성이다.
부모 노드는 자식 노드보다 우선 순위가 높아야 한다.
BinaryHeap은 불변성을 유지하기 위해 sift_up(), sift_down() 함수를 중심으로 동작한다.
내부 구현을 보면 이진 힙으로 구현됐다는 사실을 문서 설명이 아니라 이 두 함수에서 직접 확인할 수 있다.
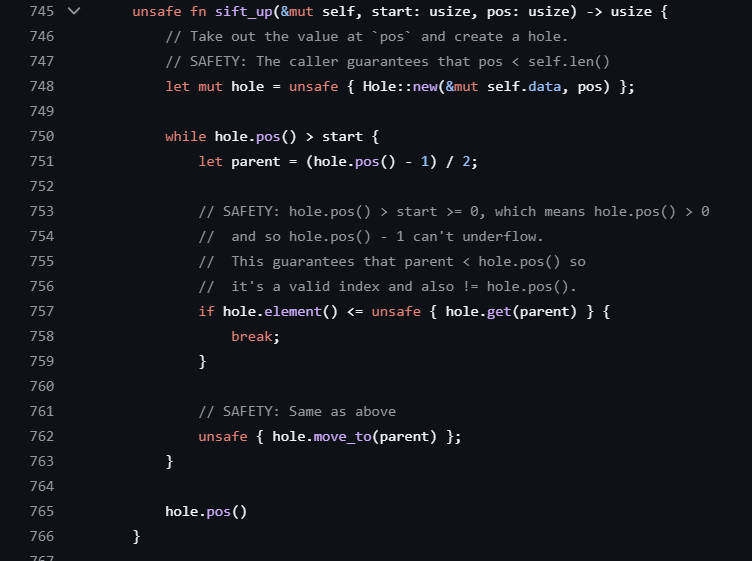
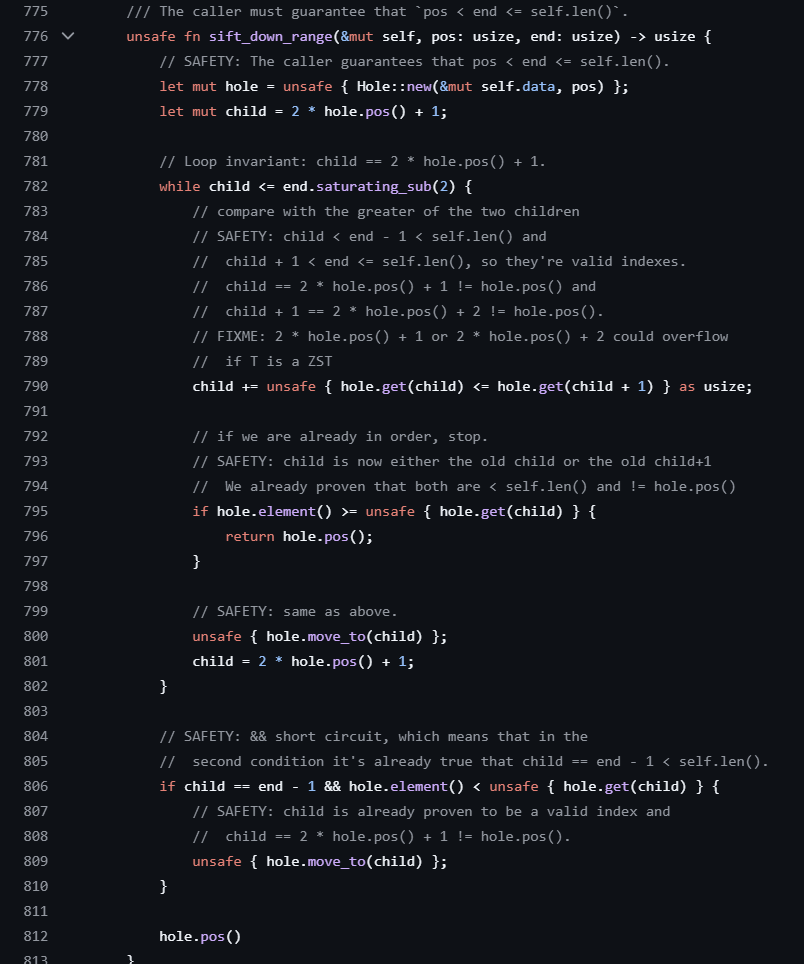
간략히 설명하면, sift_up()은 새로운 원소 삽입 시 힙 불변성을 복구하는 함수고,
sift_down()은 원소 삭제 시 힙 불변성을 복구하는 함수다.
sift_up() - 삽입 시 위로 끌어올리기
unsafe fn sift_up(&mut self, start: usize, pos: usize) -> usize {
let mut hole = unsafe { Hole::new(&mut self.data, pos) };
while hole.pos() > start {
let parent = (hole.pos() - 1) / 2;
if hole.element() <= unsafe { hole.get(parent) } {
break;
}
unsafe { hole.move_to(parent) };
}
hole.pos()
}
새 원소가 pos(Vec 맨 끝)에 추가된 직후에는 힙 불변성 원칙에 맞지 않을 수 있으니,
현재 노드와 부모 노드를 비교해서 부모보다 크다면(최대 힙이니까) 교체하면서 위로 올라간다.
parent를 찾을 때 사용하는 (hole.pos() - 1) / 2에서 앞에서 봤던 인덱스 구조가 드러난다.
👉 아래에서 위로 올라가면서 맞는 자리를 찾아가는 과정의 반복이다.
sift_down() - 삭제 시 아래로 내려 보내기
unsafe fn sift_down_range(&mut self, pos: usize, end: usize) -> usize {
let mut hole = unsafe { Hole::new(&mut self.data, pos) };
let mut child = 2 * hole.pos() + 1;
while child <= end.saturating_sub(2) {
child += unsafe { hole.get(child) <= hole.get(child + 1) } as usize;
if hole.element() >= unsafe { hole.get(child) } {
return hole.pos();
}
unsafe { hole.move_to(child) };
child = 2 * hole.pos() + 1;
}
if child == end - 1 && hole.element() < unsafe { hole.get(child) } {
unsafe { hole.move_to(child) };
}
hole.pos()
}
unsafe fn sift_down(&mut self, pos: usize) -> usize {
let len = self.len();
unsafe { self.sift_down_range(pos, len) }
}
기존 루트를 제거한 뒤, Vec의 마지막 원소를 루트로 올린다.
이때의 루트는 자식보다 작을 수 있어서 힙 불변성이 깨진 상태이니,
먼저 현재 노드의 왼쪽 자식 노드와 오른쪽 자식 노드 중 우선순위가 높은 쪽을 선택하고,
그 자식 노드보다 작다면 자리를 교체해 아래로 이동하면서 자리를 찾아나가는 과정을 반복한다.
let mut child = 2 * hole.pos() + 1;
...
child += unsafe { hole.get(child) <= hole.get(child + 1) } as usize;child에서의 (hole.pos() * 2) + 1의 구조와 오른쪽 노드를 child + 1로 표현하는 걸 볼 수 있다.
unsafe fn sift_down_range(&mut self, pos: usize, end: usize) -> usize {
...
}
unsafe fn sift_down(&mut self, pos: usize) -> usize {
let len = self.len();
unsafe { self.sift_down_range(pos, len) }
}한 가지 눈에 띄는 점은 실제 구현이 sift_down_range()에 있고,
sift_down()은 이를 감싸는 래퍼 형태라는 점이다.
이렇게 분리한 이유는 sift_down()연산이 항상 힙 전체에만 적용되는 게 아니라서 그렇다.
일반적인 힙 연산(push(), pop(), rebuild())에서는 Vec 전체가 힙이니 따질 필요가 없었다.
정렬 알고리즘 중 힙 정렬(heap sort)을 들어봤을 것이다.
into_sorted_vec()은 내부적으로 힙 정렬을 사용하는데 여기선 상황이 다르다.
#[must_use = "`self` will be dropped if the result is not used"]
#[stable(feature = "binary_heap_extras_15", since = "1.5.0")]
pub fn into_sorted_vec(mut self) -> Vec<T, A> {
let mut end = self.len();
while end > 1 {
end -= 1;
unsafe {
let ptr = self.data.as_mut_ptr();
ptr::swap(ptr, ptr.add(end));
}
unsafe { self.sift_down_range(0, end) };
}
self.into_vec()
}
루트를 맨 뒤로 보내고, 힙의 유효 범위(end)를 하나씩 줄여나가면서
줄어든 범위 내에서만 힙 불변성을 복구하는 걸 볼 수 있다.
이게 뭔 소리냐면,
[ 힙 영역 (0 .. end-1) | 정렬된 영역 (end .. len-1) ]이런 상태인 것이다.
뒤쪽 영역은 정렬이 끝났기 때문에 힙 연산에 포함하지 않는 것이다.
최소 힙으로 바꾸는 법
앞서 설명했듯이 Rust의 BinaryHeap은 기본적으로 최대 힙이다.
Ord 트레이트의 비교 결과를 그대로 사용하기 때문이다.
그 말은?
최소 힙으로 바꾸고 싶다면 비교 결과를 뒤집으면 된다는 말이다.
Either core::cmp::Reverse or a custom Ord implementation can be used to make BinaryHeap a min-heap.
This makes heap.pop() return the smallest value instead of the greatest one.
use std::collections::BinaryHeap;
use std::cmp::Reverse;
let mut heap = BinaryHeap::new();
heap.push(Reverse(1));
heap.push(Reverse(5));
heap.push(Reverse(2));
assert_eq!(heap.pop(), Some(Reverse(1)));
assert_eq!(heap.pop(), Some(Reverse(2)));
assert_eq!(heap.pop(), Some(Reverse(5)));
assert_eq!(heap.pop(), None);비교 결과를 뒤집는 래퍼 타입인 Reverse<T>를 사용하거나 커스텀으로 구현하면 된다.
힙을 건드리는 게 아니라 값 쪽에서 비교 정책을 해결한다는 점을 여기서 또 한번 확인할 수 있다.
메서드 종류와 사용법 (총 11가지)
(1) BinaryHeap 생성 - ::new() / ::with_capacity(size)
impl<T: Ord> BinaryHeap<T> {
/// ```
/// use std::collections::BinaryHeap;
/// let mut heap = BinaryHeap::new();
/// heap.push(4);
/// ```
#[stable(feature = "rust1", since = "1.0.0")]
#[rustc_const_stable(feature = "const_binary_heap_constructor", since = "1.80.0")]
#[must_use]
pub const fn new() -> BinaryHeap<T> {
BinaryHeap { data: vec![] }
}주석의 구현 예시와 같이 BinaryHeap::new() 형태로 사용하면 된다.
코드와 같이 new()는 내부적으로 빈 Vec을 가진 힙을 반환한다.
/// ```
/// use std::collections::BinaryHeap;
/// let mut heap = BinaryHeap::with_capacity(10);
/// heap.push(4);
/// ```
#[stable(feature = "rust1", since = "1.0.0")]
#[must_use]
pub fn with_capacity(capacity: usize) -> BinaryHeap<T> {
BinaryHeap { data: Vec::with_capacity(capacity) }
}미리 내부 Vec 용량을 확보하고 싶다면 with_capacity(size)를 사용하면 된다.
원소 할당을 많이 할 것 같을 때 이렇게 미리 확보해두면 재할당을 줄여 성능상 이득이다.
(2) 원소 삽입 - .push(value)
/// # Time complexity
///
/// The expected cost of `push`,... is *O*(1).
/// ...
/// The worst case cost of a *single* call to `push` is *O*(*n*).
#[stable(feature = "rust1", since = "1.0.0")]
#[rustc_confusables("append", "put")]
pub fn push(&mut self, item: T) {
let old_len = self.len();
self.data.push(item);
// SAFETY: Since we pushed a new item it means that
// old_len = self.len() - 1 < self.len()
unsafe { self.sift_up(0, old_len) };
}
// ------ 아래 사용 예시
use std::collections::BinaryHeap;
let mut heap = BinaryHeap::new();
heap.push(3);
heap.push(5);
heap.push(1);
assert_eq!(heap.len(), 3);
assert_eq!(heap.peek(), Some(&5));위에서 살펴봤듯이 내부적으로 sift_up()을 사용하는 것을 볼 수 있다.
맨 끝에 추가하고 자리를 찾아 올라가는 과정이 있어서
시간 복잡도는 평균 O(1)에서 최악 O(log n)까지 가능하다.
내부 코드를 보면 아주 훌륭하게도 Time Complexity가 주석으로 표기되어 있다 👍
(3) 루트 제거 - .pop()
/// # Time complexity
///
/// The worst case cost of `pop` on a heap containing *n* elements is *O*(log(*n*)).
#[stable(feature = "rust1", since = "1.0.0")]
pub fn pop(&mut self) -> Option<T> {
self.data.pop().map(|mut item| {
if !self.is_empty() {
swap(&mut item, &mut self.data[0]);
// SAFETY: !self.is_empty() means that self.len() > 0
unsafe { self.sift_down_to_bottom(0) };
}
item
})
}
// ------------ 아래는 사용 예시
use std::collections::BinaryHeap;
let mut heap = BinaryHeap::from([1, 3]);
assert_eq!(heap.pop(), Some(3));
assert_eq!(heap.pop(), Some(1));
assert_eq!(heap.pop(), None);
내부적으로 sift_down() 쓴다면서 sift_down_to_bottom() 뭐임?
이 부분은 사실 성능 최적화가 들어가서 그렇다.
self.data.pop().map(|mut item| {일단 이 부분에서 Vec의 마지막 원소를 꺼내서 item으로 소유권을 전달하고 있다.
if !self.is_empty() {
swap(&mut item, &mut self.data[0]);그리고 여기서 힙이 비어있지 않다면 마지막 원소와 루트를 교체한다.
(비어있으면 마지막으로 꺼낸 걔가 루트였던 거다)
그러면 루트 값이 item으로 들어가고, 루트 자리에 마지막 원소가 위치한 상태가 된다.
이 상태에서 sift_down_to_bottom()을 살펴보자.
unsafe fn sift_down_to_bottom(&mut self, mut pos: usize) {
let end = self.len();
let start = pos;
let mut hole = unsafe { Hole::new(&mut self.data, pos) };
let mut child = 2 * hole.pos() + 1;
while child <= end.saturating_sub(2) {
child += unsafe { hole.get(child) <= hole.get(child + 1) } as usize;
unsafe { hole.move_to(child) };
child = 2 * hole.pos() + 1;
}
if child == end - 1 {
unsafe { hole.move_to(child) };
}
pos = hole.pos();
drop(hole);
unsafe { self.sift_up(start, pos) };
}루트에 마지막 원소(힙에서 가장 작을 확률이 높음)가 들어가 있으니 힙 불변성을 복구해야 한다.
일반적인 sift_down()과는 다르게 힙의 마지막 원소였다는 특성상,
중간에서 멈추지 않고 아래로 계속해서 내려가게 될 것이다.
while child <= end.saturating_sub(2) {
child += unsafe { hole.get(child) <= hole.get(child + 1) } as usize;
unsafe { hole.move_to(child) };
child = 2 * hole.pos() + 1;
}그 특성을 활용해서 매 단계마다 더 큰 자식만 골라서 무조건 이동한다.
sift_down()에서는 선별된 자식과 또 한번 비교했었다.
일단 바닥까지 내려보내겠다는 마인드로 비교 생략하고 바로 바꾸는 것이다.
if child == end - 1 {
unsafe { hole.move_to(child) };
}
pos = hole.pos();
drop(hole);
unsafe { self.sift_up(start, pos) };그렇게 바닥에 도착하면 sift_up()을 한 번 호출해서 정확한 위치를 조정한다.
기존 sift_down() 대비 비교를 최소화해서 분기를 감소시켜 성능을 향상시킨다.
이제는 pop()의 시간복잡도가 O(log n)이라는 걸 자연스레 이해할 수 있을 것이다.
(4) 루트 조회 - .peek()
/// # Time complexity
///
/// Cost is *O*(1) in the worst case.
#[must_use]
#[stable(feature = "rust1", since = "1.0.0")]
pub fn peek(&self) -> Option<&T> {
self.data.get(0)
}
// --------- 아래 사용 예시
use std::collections::BinaryHeap;
let mut heap = BinaryHeap::new();
assert_eq!(heap.peek(), None);
heap.push(1);
heap.push(5);
heap.push(2);
assert_eq!(heap.peek(), Some(&5));내부가 매우 간단한 걸 볼 수 있다.
지금까지의 흐름을 잘 따라왔다면 너무 당연하게 이해될 것이다.
바로 힙의 루트만 O(1)로 딸깍하면 끝이라는 걸 이제는 쉽게 알 수 있다.
여기서 눈여겨 볼 부분은 한 가지다.
pub fn peek(&self) -> Option<&T> {타입을 &T로 불변 참조 형태로 반환해서 조회만 가능하고 수정은 불가능하게 제한한다.
(5) 루트 수정 - .peek_mut() ⚠️
/// # Time complexity
///
/// If the item is modified then the worst case time complexity is *O*(log(*n*)),
/// otherwise it's *O*(1).
#[stable(feature = "binary_heap_peek_mut", since = "1.12.0")]
pub fn peek_mut(&mut self) -> Option<PeekMut<'_, T, A>> {
if self.is_empty() { None } else { Some(PeekMut { heap: self, original_len: None }) }
}
// ---------- 아래는 사용 예시
use std::collections::BinaryHeap;
let mut heap = BinaryHeap::new();
assert!(heap.peek_mut().is_none());
heap.push(1);
heap.push(5);
heap.push(2);
if let Some(mut val) = heap.peek_mut() {
*val = 0;
}
assert_eq!(heap.peek(), Some(&2));peek()과는 다르게 반환 타입으로 가변 참조를 제공한다.
그냥 쌩 &mut로 넘기는 건 아니고 PeekMut<>라는 래퍼 타입으로 넘긴다.
루트 값을 수정한다는 건 힙 불변성을 깨뜨릴 수 있는 만큼 위험한 행위다.
그래서 PeekMut 래퍼 타입으로 정해둔 행동을 할 수 있게 구현해뒀다.
#[stable(feature = "binary_heap_peek_mut", since = "1.12.0")]
impl<T: Ord, A: Allocator> Drop for PeekMut<'_, T, A> {
fn drop(&mut self) {
if let Some(original_len) = self.original_len {
unsafe { self.heap.data.set_len(original_len.get()) };
unsafe { self.heap.sift_down(0) };
}
}
}Drop 말고도 더 있는데 지금 맥락에서 중요한 건 drop()이다 (나머지 궁금하면 직접 볼 것)
drop()하면 자동으로 sift_down()을 호출하도록 구현해서 힙 불변성을 유지하도록 했다는 거다.
(6) 길이/상태 확인 - .len() / is_empty()
#[must_use]
#[stable(feature = "rust1", since = "1.0.0")]
#[rustc_confusables("length", "size")]
pub fn len(&self) -> usize {
self.data.len()
}
// ------ 아래는 사용 예시
use std::collections::BinaryHeap;
let heap = BinaryHeap::from([1, 3]);
assert_eq!(heap.len(), 2);len()은 usize 타입으로 길이를 반환하는 메서드다.
#[must_use]
#[stable(feature = "rust1", since = "1.0.0")]
pub fn is_empty(&self) -> bool {
self.len() == 0
}힙 사이즈가 0이 아니면 비어있지 않다는 뜻이니,
len()을 그대로 활용해 길이가 0인지 여부를 bool 타입으로 반환한다.
(7) 힙 비우기 - .clear() 👈 내부 구현이 아주 재밌는 녀석임
#[stable(feature = "rust1", since = "1.0.0")]
pub fn clear(&mut self) {
self.drain();
}
// ------ 아래는 사용 예시
use std::collections::BinaryHeap;
let mut heap = BinaryHeap::from([1, 3]);
assert!(!heap.is_empty());
heap.clear();
assert!(heap.is_empty());비우는 clear() 사용이야 뭐 다른 컬렉션처럼 간단한데, 내부 구현을 보면 좀 희한한 부분이 있다.
왜 self.data.clear()로 내부 Vec을 바로 비우지 않고 drain을 호출할까?
결과적으로 보면 둘 다 모든 원소를 제거하는 건 맞는데, 이상하게 느껴졌다.
#[inline]
#[stable(feature = "drain", since = "1.6.0")]
pub fn drain(&mut self) -> Drain<'_, T, A> {
Drain { iter: self.data.drain(..) }
}BinaryHeap drain()은 내부적으로 Vec의 drain()을 그대로 사용한다.
drain()은 반환타입이 있는 꺼내기, clear()는 비우기다.
아니, 이럴 거면 그냥 바로 Vec::clear 쓰지 왜 drain 쓴 거지?
[현재 구조] BinaryHeap의 clear() -> BinaryHeap의 drain() -> Vec의 drain()
vs
[내 생각] BinaryHeap의 clear() -> Vec의 clear()이런 구도로 보여서 굳이 돌아간다고 생각했다.
그래서 rust-lang 레포의 issue들과 pr을 뒤져보고, 공식문서를 찾다가 실마리를 잡았다.
결론부터 말하면 drain()은 비우는 과정이 아니라, 컨테이너를 즉시 비운 상태로 만든다.
이 차이 때문에 BinaryHeap는 clear()를 drain()으로 구현했다고 본다.
일단 BinaryHeap은 단순한 Vec 래퍼 타입이 아니고 힙 불변성을 유지해야하는 구조다.
그러나 clear()를 실행하는 도중 panic이 발생하면 일부 노드들만 남아서 힙 불변성이 애매해진다.
While conceptually it's simpler to state that the removal happens unconditionally and immediately, which corresponds to the verb "drain", like BinaryHeap::drain and HashMap::drain do.
<https://github.com/rust-lang/rust/issues/92765> 발췌
HashMap과 BinaryHeap, Vec의 drain()은 무조건적이고 즉각적으로 제거된다는 말이 key였다.
실제로 그렇다기 보다는 상태를 먼저 확정지은 뒤 drop()을 수행하는 형태다.
그래서 개념적으로 즉각적이고 무조건적인 제거와 가깝다.
그러니 panic이 발생해도 컨테이너는 비어있는 상태가 되니 문제가 사라진다.
The returned iterator keeps a mutable borrow on the heap to optimize its implementation.
<https://doc.rust-lang.org/std/collections/struct.BinaryHeap.html#method.drain> 발췌
mutable 참조를 반환하니까 drain iterator가 살아있는 동안 힙에 대한 다른 연산을 차단하고,
iterator drop 시엔 모든 자원이 정리되니까 안전한 메커니즘이라는 것이다.
👉 정리하면 BinaryHeap의 clear()가 drain()을 사용하는 이유는
panic 상황에서도 힙 불변성을 유지하기 위한 의도적인 선택이었던 것이다.
(8) 원소 다중 삽입 - extend()
#[inline]
fn extend<I: IntoIterator<Item = T>>(&mut self, iter: I) {
let guard = RebuildOnDrop { rebuild_from: self.len(), heap: self };
guard.heap.data.extend(iter);
}
// ------ 아래는 사용 예시
use std::collections::BinaryHeap;
let mut heap = BinaryHeap::new();
heap.extend([3, 1, 4, 2]);
assert_eq!(heap.peek(), Some(&4));여러 원소를 한번에 추가할 때 사용하는 메서드다.
그런데 내부적으로 push()를 반복 호출하지 않는다.
sift_up 같은 힙 연산도 보이지 않는데 어떻게 추가한다는 걸까?
기존에 힙 불변성이 유지된 상태의 힙 인덱스 이후로 guard를 세워두고
내부 Vec::extend를 호출하는데 이 시점엔 어쩔 수 없이 힙 불변성이 깨지게 된다.
그렇지만 guard가 mutual borrow를 유지하고 있으니까 괜찮다.
struct RebuildOnDrop<
'a,
T: Ord,
#[unstable(feature = "allocator_api", issue = "32838")] A: Allocator = Global,
> {
heap: &'a mut BinaryHeap<T, A>,
rebuild_from: usize,
}
impl<T: Ord, A: Allocator> Drop for RebuildOnDrop<'_, T, A> {
fn drop(&mut self) {
self.heap.rebuild_tail(self.rebuild_from);
}
}extend()가 끝나고 나면 guard가 drop되는데 (RAII기반 Drop 가드)
이때 RebuildOnDrop 내부에서 rebuild_tail()이 사용된다.
이게 뭐냐면 기존에 힙 불변성이 유지된 부분은 그대로 사용하고,
새로 붙은 부분(tail)만 힙에 편입하겠다는 의미로 끝부분에서 필요한 만큼만 복구한다.
- push x 100번 → sift_up 100번 ❌
- extend 100개 → Vec append 1번 → rebuild_tail 1번 ⭕원소들을 물리적으로 한번에 힙에 다 넣겠다는 게 아니다.
👉 성능 향상을 위해서 Vec::extend로 물리적으로 원소들을 추가한 다음에,
RebuildOnDrop에서 논리적으로 힙에 편입해 힙 복구를 한번에 처리한다는 뜻이다.
(9) Vec로 힙 생성 - .from(Vec) / FromIterator
extend()로 여러 원소를 한번에 추가할 때 복구를 묶어서 처리하는 걸 봤다.
그럼 아예 초기 데이터로 힙을 생성하려면 어떻게 할까?
#[stable(feature = "binary_heap_extras_15", since = "1.5.0")]
impl<T: Ord, A: Allocator> From<Vec<T, A>> for BinaryHeap<T, A> {
/// Converts a `Vec<T>` into a `BinaryHeap<T>`.
///
/// This conversion happens in-place, and has *O*(*n*) time complexity.
fn from(vec: Vec<T, A>) -> BinaryHeap<T, A> {
let mut heap = BinaryHeap { data: vec };
heap.rebuild();
heap
}
}From<Vec<T>>은 초기 데이터를 O(n)에 힙으로 쉽게 변환할 수 있게 해준다.
내부적으로는 기존 Vec을 그대로 재사용하고 rebuild()를 호출해 힙을 구성하는데,
이 방식은 추가적인 메모리 할당이 없고 push()를 반복 호출하지 않아 효율적이다.
#[stable(feature = "rust1", since = "1.0.0")]
impl<T: Ord> FromIterator<T> for BinaryHeap<T> {
fn from_iter<I: IntoIterator<Item = T>>(iter: I) -> BinaryHeap<T> {
BinaryHeap::from(iter.into_iter().collect::<Vec<_>>())
}
}FromIterator<T>도 내부적으로 from()으로 귀결되는 것을 볼 수 있다.
(10) 힙 정렬 - .into_sorted_vec()
sift_down_range() 설명하면서 다뤘던 바로 그 녀석이다.
#[must_use = "`self` will be dropped if the result is not used"]
#[stable(feature = "binary_heap_extras_15", since = "1.5.0")]
pub fn into_sorted_vec(mut self) -> Vec<T, A> {
let mut end = self.len();
while end > 1 {
end -= 1;
unsafe {
let ptr = self.data.as_mut_ptr();
ptr::swap(ptr, ptr.add(end));
}
unsafe { self.sift_down_range(0, end) };
}
self.into_vec()
}
// --- 아래는 사용 예시
use std::collections::BinaryHeap;
let mut heap = BinaryHeap::from([3, 1, 4, 2]);
let sorted = heap.into_sorted_vec();
assert_eq!(sorted, vec![1, 2, 3, 4]);BinaryHeap을 소비해서 오름차순으로 정렬된 Vec을 반환한다.
앞서 설명한 것처럼 루트와 마지막 요소를 swap하고,
end 범위를 좁혀가면서 sift_down_range()를 반복하는 전형적인 힙 정렬이다.
n개 원소가 log n 작업을 반복하니, 시간 복잡도는 O(n log n)이다.
(11) (정렬 없는) 힙 내부 원소 순회 - .iter()
#[stable(feature = "rust1", since = "1.0.0")]
#[cfg_attr(not(test), rustc_diagnostic_item = "binaryheap_iter")]
pub fn iter(&self) -> Iter<'_, T> {
Iter { iter: self.data.iter() }
}
// ------- 아래는 사용 예시
use std::collections::BinaryHeap;
let heap = BinaryHeap::from([1, 2, 3, 4]);
// Print 1, 2, 3, 4 in arbitrary order
for x in heap.iter() {
println!("{x}");
}
앞서 얘기했듯 BinaryHeap 내부는 정렬된 상태가 아니다.
그래서 순회 결과도 힙 순서가 아니라 그냥 내부 Vec에 있는 순서다.
디버깅할 때 내부에 뭐있나 확인하는 용도로 쓰기 좋을 것 같다.
🪄 요약 & 마무리
1. BinaryHeap은 Vec 기반 최대 힙으로 구현된 우선순위 큐다.
2. 내부적으로 sift_up, sift_down을 사용해 힙 불변성을 유지한다.
3. 비교 정책을 값의 Ord에 맡기고, 힙은 그 결과만 소비하는 구조로 책임을 분리했다.
4. 메서드 내부 구현에 성능 향상과 힙 불변성 유지를 위한 최적화 코드가 많다.
솔직히 여기까지 알면 Rust 사용하면서 BinaryHeap를 활용하는덴 전혀 문제 없고,
Rust에서 BinaryHeap이 어떻게 돌아가는지 충분히 이해하고 쓴다고 볼 수 있다.
그래도 궁금한 점 있으면 댓글 남겨주고,
혹시 글에서 틀린 부분이 있었거나 피드백을 남겨주신다면 매우 감사하게 받겠습니다.
나는 내부가 더 궁금하다! 하는 분들은 아래 참고 자료에 공식문서랑 내부 코드 링크 뒀으니까 직접 파헤쳐보시길
📌 참고 자료
1) Rust 공식문서: BinaryHeap in std::collections
https://doc.rust-lang.org/std/collections/struct.BinaryHeap.html
BinaryHeap in std::collections - Rust
Tries to reserve the minimum capacity for at least additional elements more than the current length. Unlike try_reserve, this will not deliberately over-allocate to speculatively avoid frequent allocations. After calling try_reserve_exact, capacity will be
doc.rust-lang.org
2) rust-lang 오픈 소스: binary_heap 내부 코드
https://github.com/rust-lang/rust/blob/main/library/alloc/src/collections/binary_heap/mod.rs
rust/library/alloc/src/collections/binary_heap/mod.rs at main · rust-lang/rust
Empowering everyone to build reliable and efficient software. - rust-lang/rust
github.com
'Rust 연구 노트 > Rust 이야기' 카테고리의 다른 글
| [Rust/도서 리뷰] <이지 러스트> (9) | 2025.03.31 |
|---|---|
| [Rust] 함수 시그니처 lifetime에 대한 고찰 (0) | 2024.10.03 |
| [Rust/도서 리뷰] <러스트 프로페셔널 코드> (6) | 2024.09.10 |
| [Rust] Rust 소개, 설치 및 IDE 환경 세팅 + Cargo (0) | 2024.07.15 |