참여하고 있는 알고리듬 스터디에서 이 주제로 발표를 했었는데,
반응이 괜찮아서 여기에도 포스팅한다.
다들 15분 내로 유니온 파인드 알고리듬을 터득하게 해주겠다.
유니온 파인드가 뭐냐

먼저, 위 그림처럼 1부터 6까지의 개별 집합에 속한 각각의 노드들이 있다고 가정해보자.
개별적인 집합이므로 해당 집합의 루트 노드는 자기 자신인 상태로 볼 수 있다.

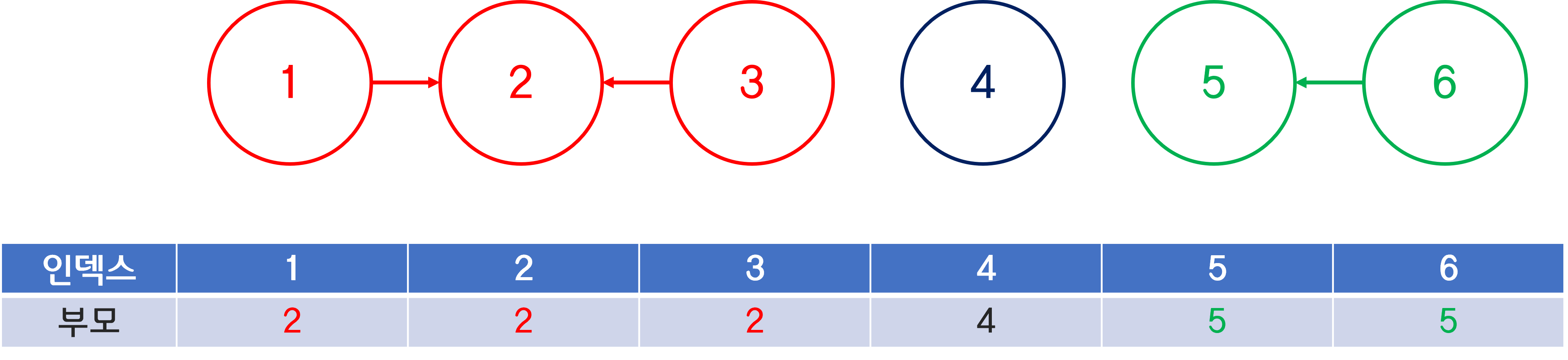
여기서 1-2-3 노드끼리 연결하고, 5-6 노드끼리 연결해서 총 세 개 집합으로 분리한다면?

상태는 이렇게 변하게 될 것이다.
지금 묶인 방향으로 보면 2번은 1번에 묶이고, 3번은 2번에 묶였으니,
1-2-3이 속한 집합에서 루트는 1이 될 것이다.
마찬가지로 4가 속한 집합은 여전히 4뿐이니 4가 루트인 집합이 되고,
5-6이 속한 집합은 6번 노드가 5번에 연결됐으므로 5가 루트인 집합이 된다.
여기서 "1-2-3 집합이고, 5-6 집합이고 왜 네 맘대로 1번을 루트로 두고, 5번을 루트로 두냐?" 싶을 수 있다.
노드가 1개였던 개별 집합에서 합집합이 일어나는 각 과정은 결국 두 노드간의 연결로 볼 수 있다.
그리고 각 노드를 연결할 때 어느 순서로 연결할 지는 정해져 있는 게 아니라서 중요하지 않다.
순전히 자기 마음이다.
오해 풀기: 트리에 방향이랑 루트는 대체 무슨 말이고 🤬

"너는 인마 무방향 트리도 모르냐! 그리고 트리에 루트가 어딨어 인마!!!!@@@!!"
이 부분이 쉽게 이해가 가지 않을 수도 있다.
알다시피 그래프 이론에서 트리는 분명 단순히 노드간 연결된 구조에 지나지 않기 때문이다.
맞다, 그래프 이론 관점에서 봤을 때 트리는 무방향이라고도 볼 수 있다.
하지만 그래프 이론을 문제 해법으로 옮겨 알고리듬에 적용시키기 위해서는 결국 자료구조를 이용해야 한다.
그러다보니 그래프 이론에서는 무방향에 루트도 따로 정해져 있지 않은 개념의 트리였지만,
자료구조적으로 표현되는 과정에서 부모-자식 관계가 나타나며 방향이 생기게 됐고,
따라서 각 집합에는 루트가 존재하게 된다.
그럼 이제 트리에 방향과 루트가 왜 존재하느냐에 대한 의문은 해소했고.
왜 부모-자식관계를 마음대로 설정하는 거냐! 그래도 되는 거냐?에 대한 이야기를 해보자.
오해 풀기 2: 부모에 어떤 노드를 두든 상관없는 이유 🧐

문제가 된 게 이 부분일 것이다.
1-2-3집합에서 왜 1을 루트로 둔 거냐? 난 2나 3이 더 좋다!! 하는 의견이 있을 수 있는데,
그럼 그렇게 하세요~
정말 자기 마음대로 해도 되는 부분이다.
왜 그걸 자기 마음대로 해도 되는가~?

신형만을 예시로 들어보겠다.
ㄷㅏ들 '짱구는 못말려'는 한번쯤 봤을 것 같다.


우리가 잘 아는 '짱구 아빠' 신형만이다.
그런데 신형만에게는 아들 짱구와 딸 짱아가 있다.
그럼 신형만은 짱구 아빠인가, 짱아 아빠인가?
짱구 아빠로 불리든, 짱아 아빠로 불리든 둘 다 맞는 말이라서 뭘로 불려도 상관이 없다.
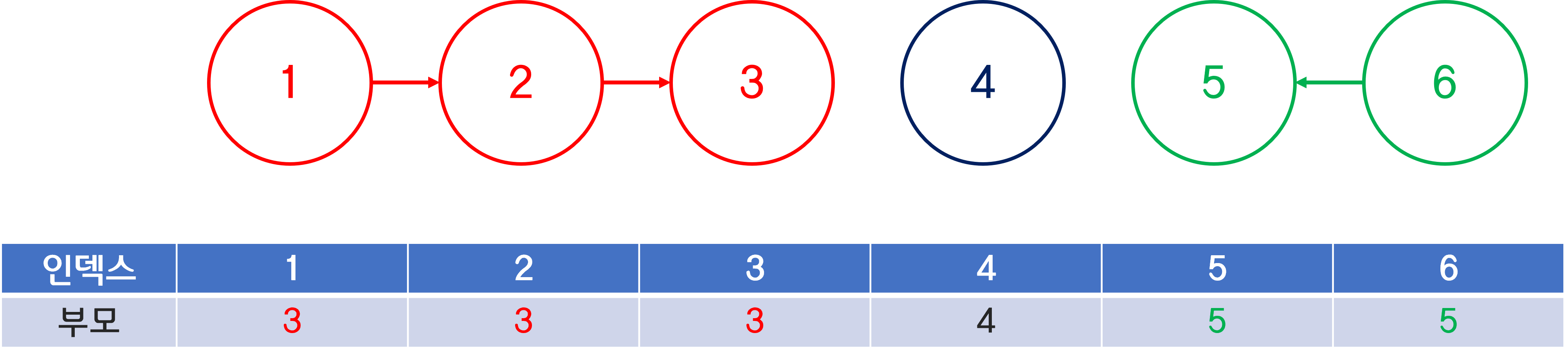
이것처럼 위의 노드에서도 2번 노드가 부모가 되든, 3번이 부모가 되든 상관없다.
이제 충분히 이해했을 것 같으니 다시 넘어가보자.
중요한 건 결국, 조상이 같은가 ⭐

우리 한국 사람은 단군 할아버지의 자손이다.
갑자기 단군 할아버지 얘기가 왜 나오는지 맥락을 모르는 사람(외국인 포함)도 있을 수 있으니
요즘 극장판도 나온 진격의 거인을 예시로 들면


'시조' 거인 유미르의 자손들은 거인이 될 수 있고, 이게 <진격의 거인> 이야기의 핵심이다.
파라디 섬이건, 마레에 사는 에르디아인이건 모두 유미르를 시조로 둔 사람들이라는 말이다.
즉, 같은 민족은 시조가 같고 동일한 시조 아래 한 민족이 구성된다는 의미다.
이걸 아까 트리 노드 집합에 적용시키면 어떻게 되겠어?
루트 노드가 같은 노드끼리는 같은 집합에 속한다는 의미가 되는 것이다.
🔎 시조를 찾는 방법 (Find)
그럼 아까의 상황으로 돌아가서,
1-2-3 집합에서 3번 노드는 자기가 속한 집합의 시조를 어떻게 찾을 수 있을까?
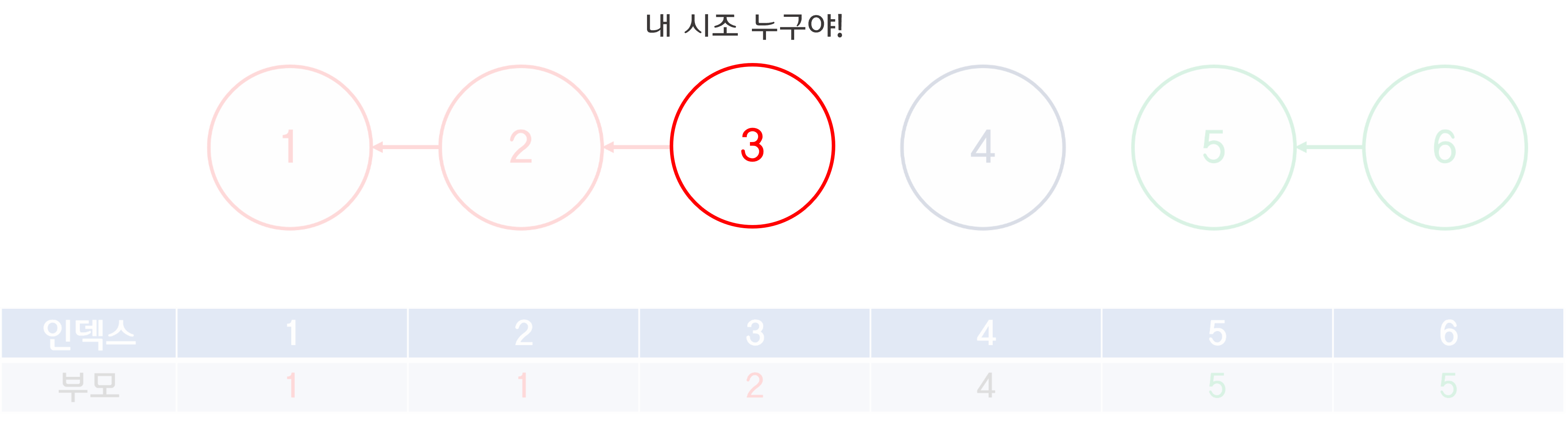
이건 노드 아래 계속 표시해왔던 부모 저장 배열을 이용하면 쉽게 알 수 있다.
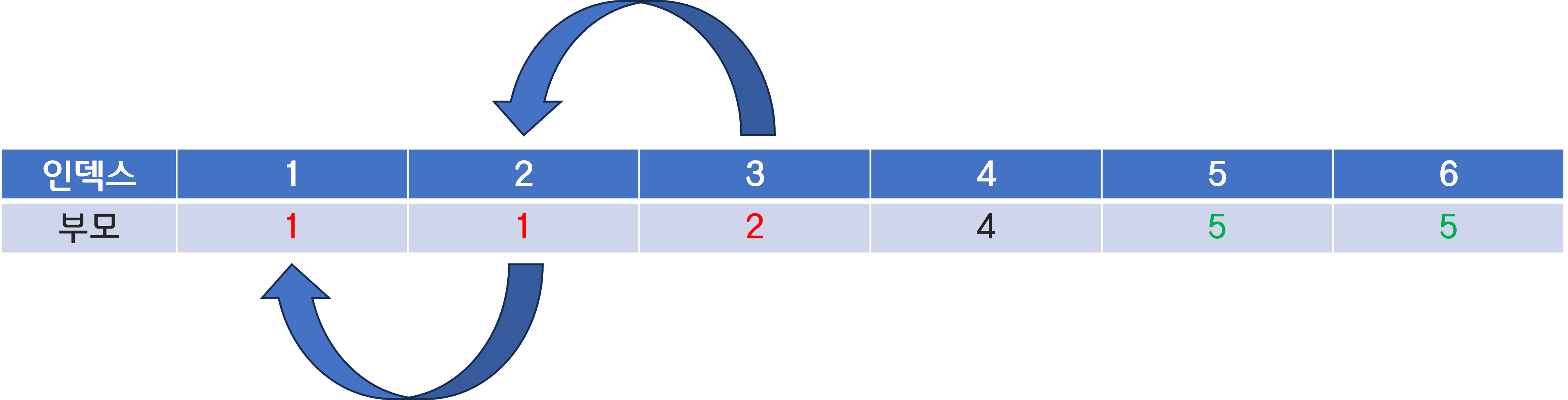
이렇게 현재 노드의 부모, 부모 노드의 부모, 부모 노드의 부모 노드의 부모, ... 를 계속 타고 올라가다 보면
결국 시조인 루트 노드가 나오게 될 것이다.
이걸 코드로 하면?
int Find(int x) {
if (root[x] == x) return x;
return Find(root[x]);
}
이렇게 자기 자신이 루트인 노드를 찾을 때까지 재귀 함수로 호출하면 되는 것이다.
➕ 그럼 합집합은 어떻게 해? (Union)
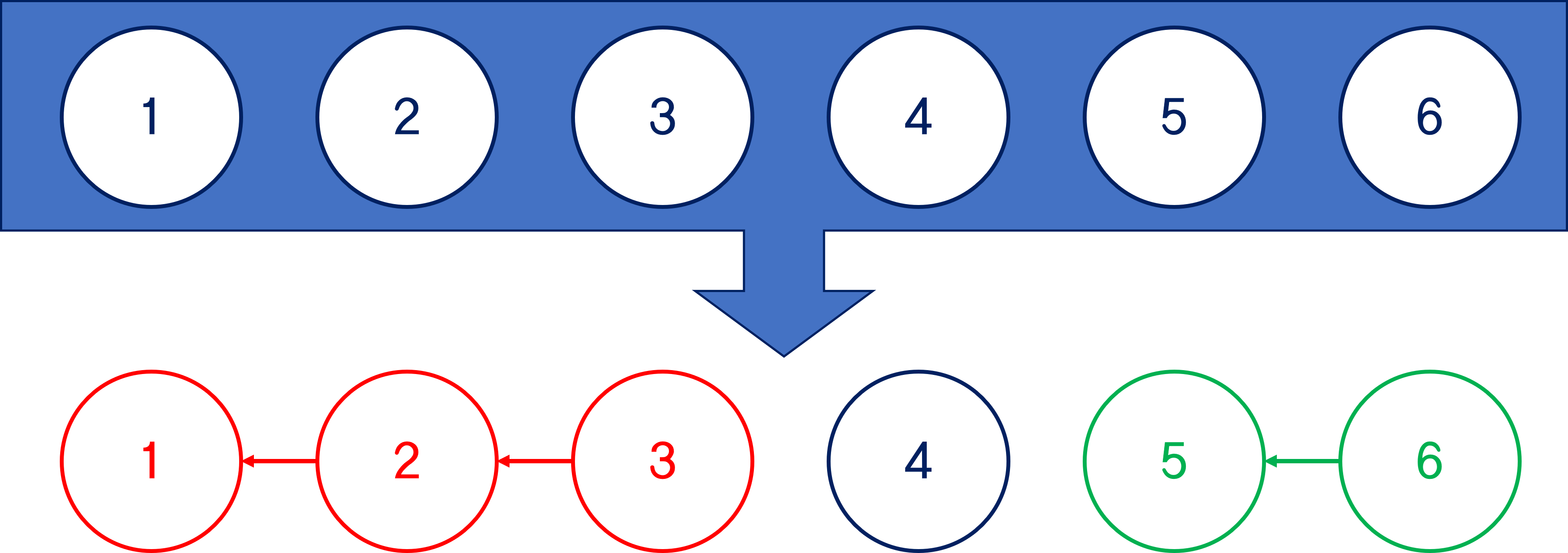
아까 최초 6개 개별 집합 상태에서 3개 집합으로 만든 이 과정은 어떻게 할까?
이것 역시 앞의 조상 찾기 시스템을 이용하면 간단하다.
void Union(int x, int y) {
int rootX = Find(x); // x의 시조.
int rootY = Find(y); // y의 시조.
if (rootX != rootY)
root[rootY] = rootX; // 이제 y의 시조는 시조가 아니다.
}
두 노드를 한 집합으로 묶으려고 할 때,
우선 각 노드의 집합을 파악하는 게 먼저일 것이다.
만약 두 노드가 이미 서로 같은 집합에 속해있다면?

이미 같은 집합이니 당연히 묶을 필요가 없을 것이다.
서로 다른 집합일 때 합집합을 하게 되는데,
각 노드의 시조가 다르다면 다른 집합에 속해있음을 알 수 있게 된다.
이후, 한 쪽의 시조를 다른 쪽 시조 아래 자식으로 둔다.
여기서 아까 말했던 짱구 아빠로 할 지, 짱아 아빠로 할 지를 쓸 수 있다.
난 그냥 x가 짱먹는 순서로 만들었다.
핵심은 시조 찾기와 합집합
// 시조 찾기.
int Find(int x) {
if (root[x] == x) return x;
return Find(root[x]);
}
// 합집합.
void Union(int x, int y) {
int rootX = Find(x); // x의 시조.
int rootY = Find(y); // y의 시조.
if (rootX != rootY)
root[rootY] = rootX; // 이제 y의 시조는 시조가 아니다.
}
사실상 이 두 가지가 유니온 파인드의 전부라고 보면 된다.
시조 찾는 Find() 함수와 합집합하는 Union() 함수는 저 형태에서 크게 벗어날 일이 없다.
저 두 개만 잘 기억해두자.
느리게 풀고 싶으면 말이지ㅋ
여기서 더 효율적으로 풀기 위한 최적화 방법이 있다.
최적화 기법
1. 경로 압축 (Path Compression) ⭐
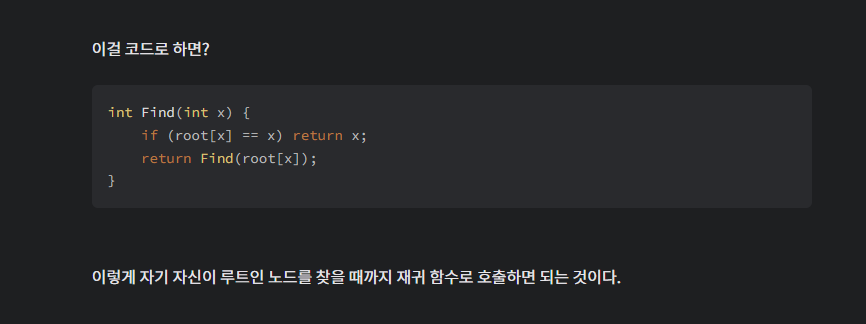
이 Find() 연산하는 코드를 다시 잘 살펴보자.
현재 노드의 부모를 찾고,
부모 노드의 부모를 찾고,
부모 노드의 부모 노드의 부모를 찾고,
부모 노드의 부모 노드의 부모 노드의 부모를 찾으면서

거의 뭐 엄마 찾아 삼만리가 되어가고 있다.
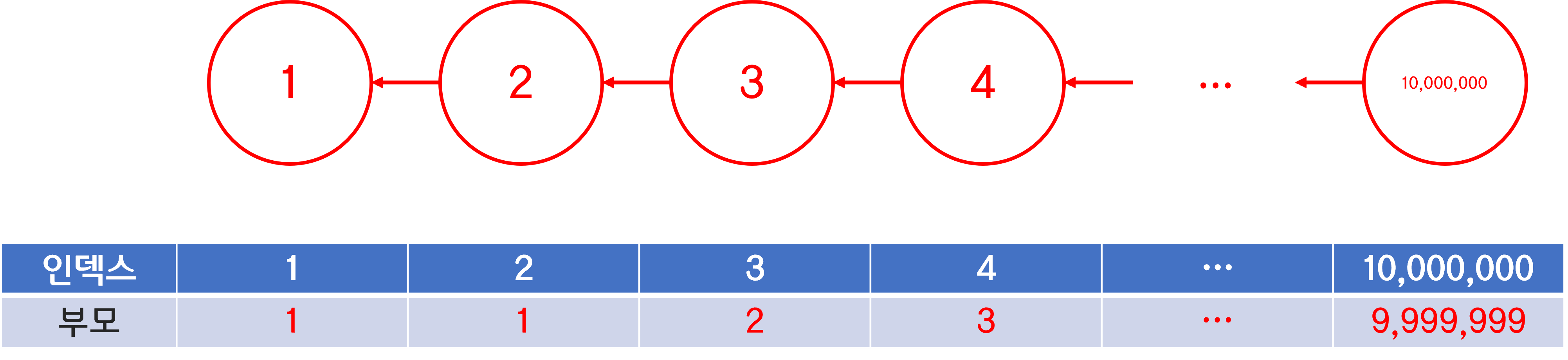
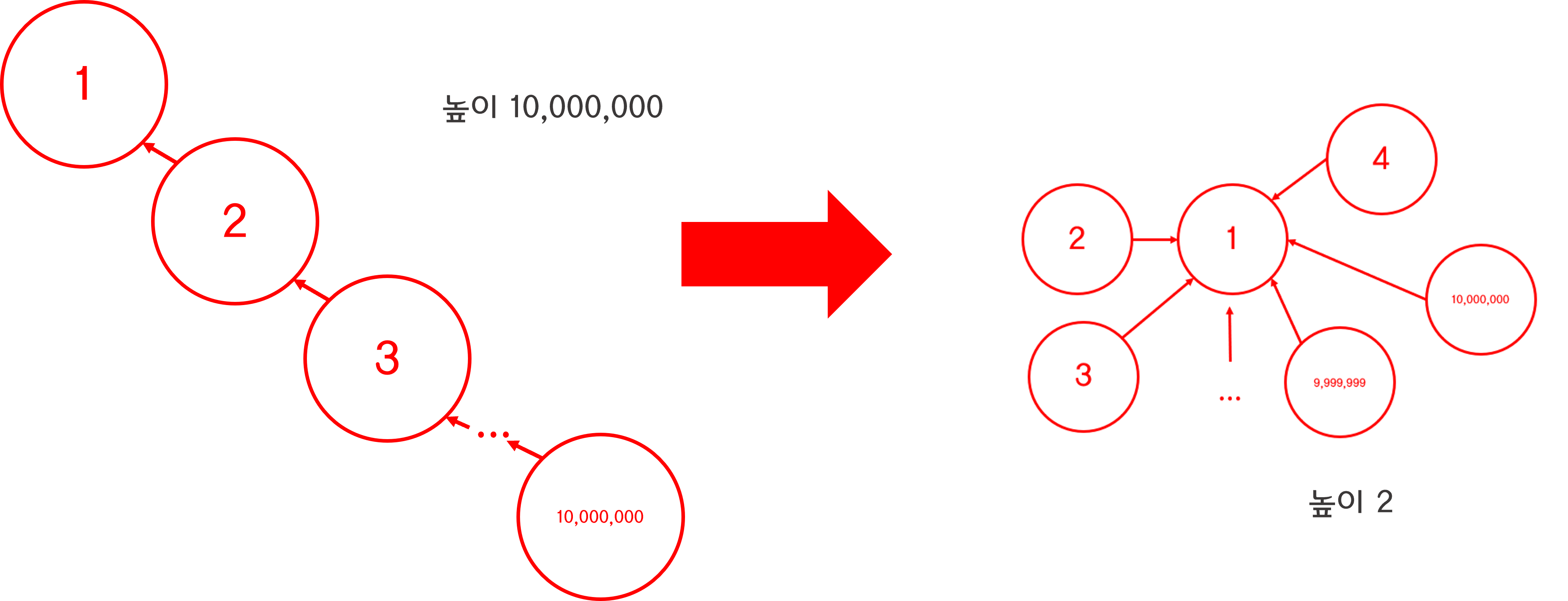
만약 이런 식으로 1번 노드를 시조로 일렬로 연결된 트리가 등장한다면,
10,000,000번 노드는 시조를 찾는 데 얼마나 걸릴까?
같은 집합인지만 보려 한건데, 이러면 조상 찾는데만 한 세월이 걸리게 된다.
이걸 어떻게 해결할 수 있을까?
만약, 시조를 찾은 직후에 Find() 재귀 함수 호출 지점으로 돌아오면서
그대로 최초 호출 지점으로 돌아가는 게 아니라

매 반환마다 그 시조 노드 값을 전파하면서 돌아온다면?!
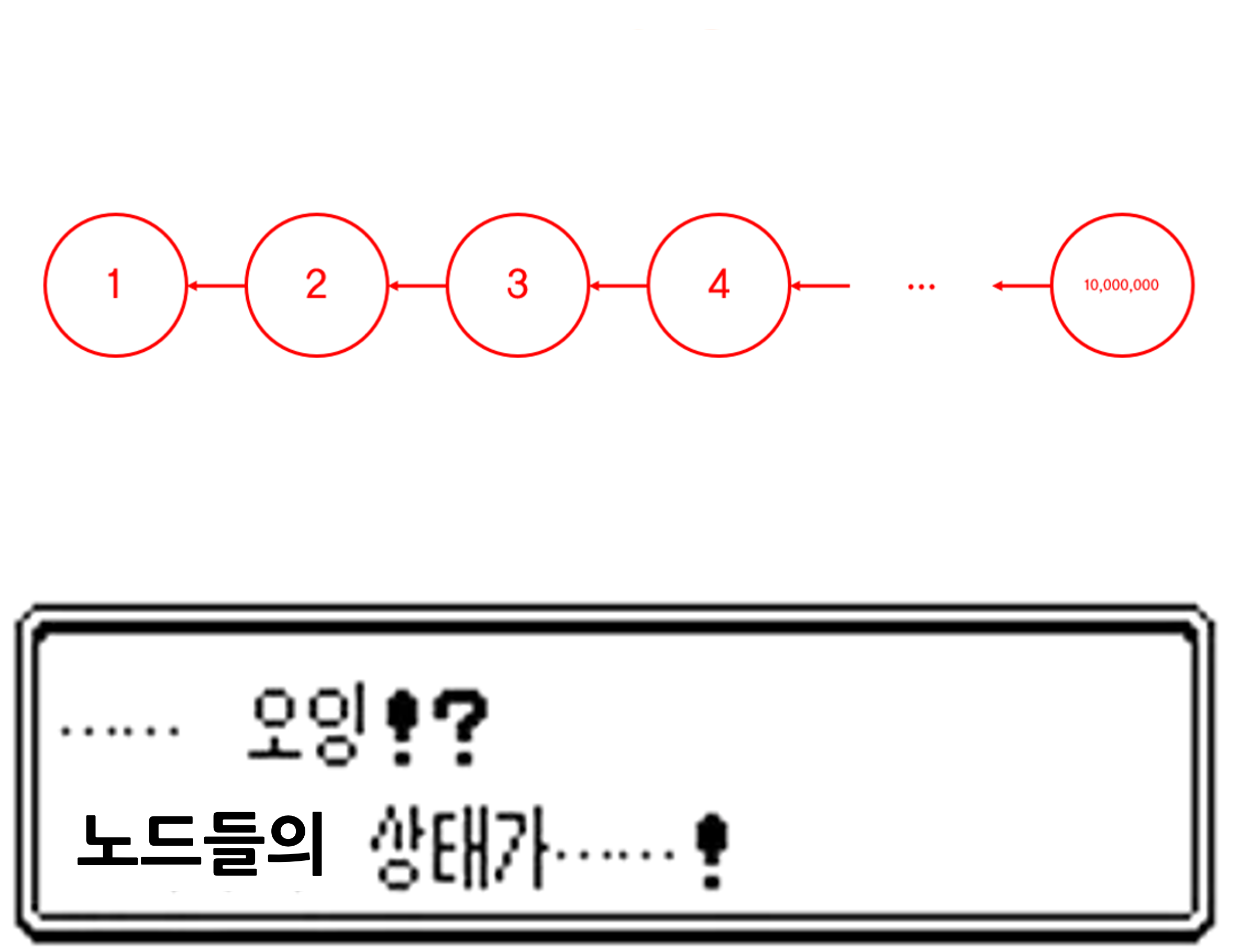
오잉!? 10,000,000층 높이 트리의 노드들의 상태가...!
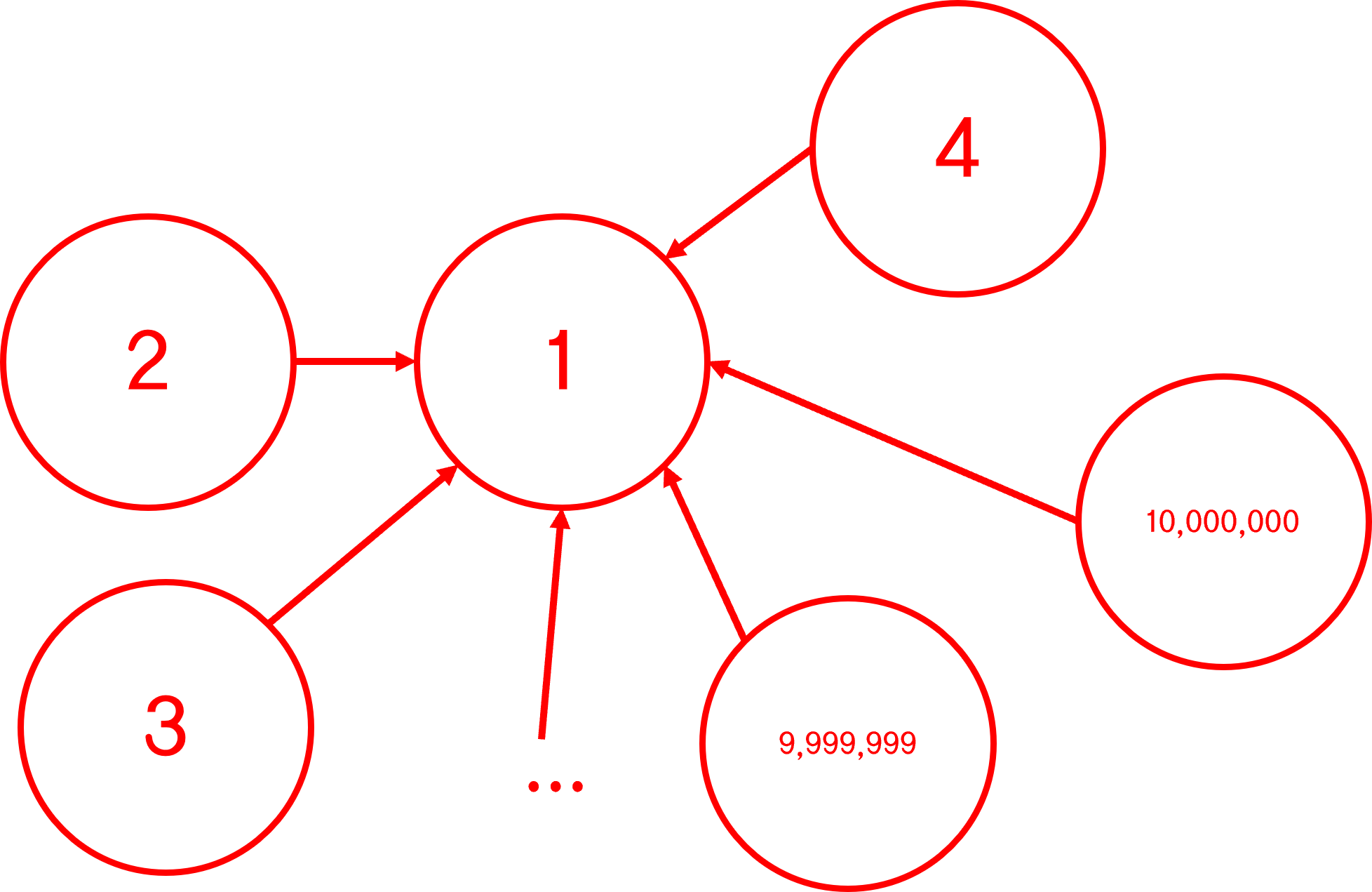
높이 2의 트리로 진화했다!
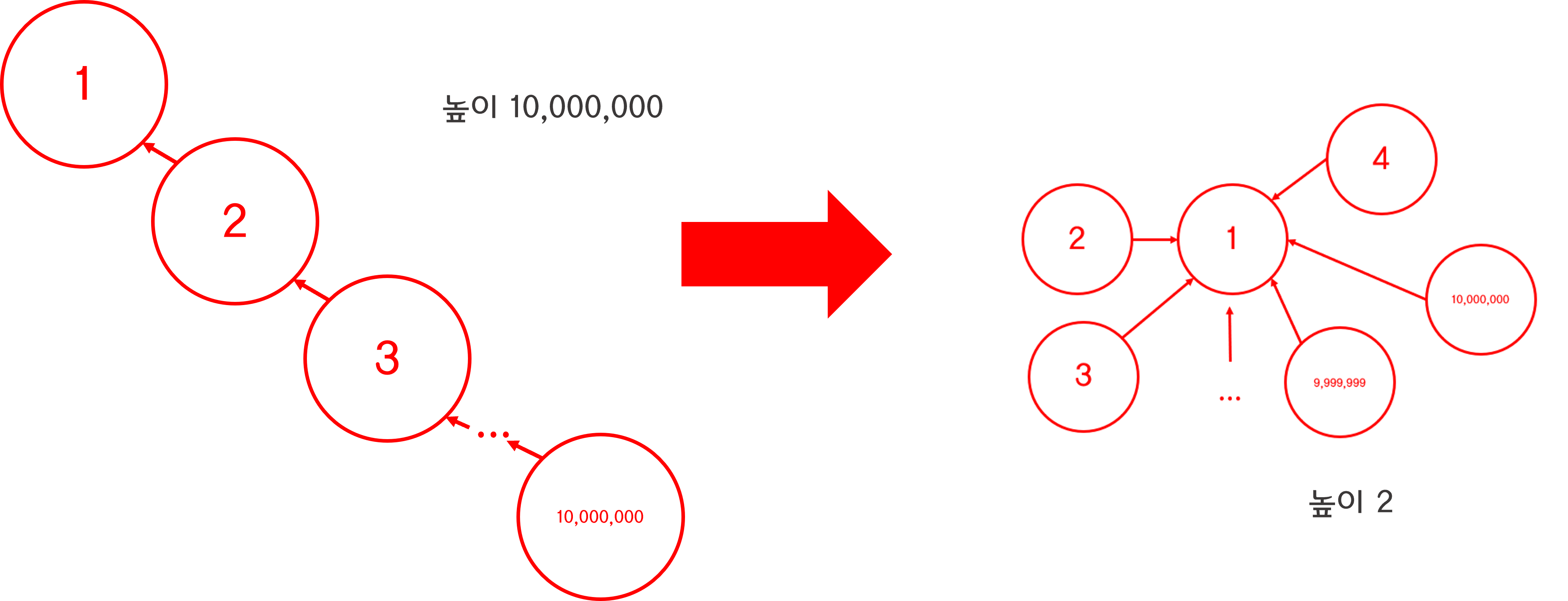
이전과 비교했을 때 현격히 트리의 높이가 낮아진 것을 알 수 있다.
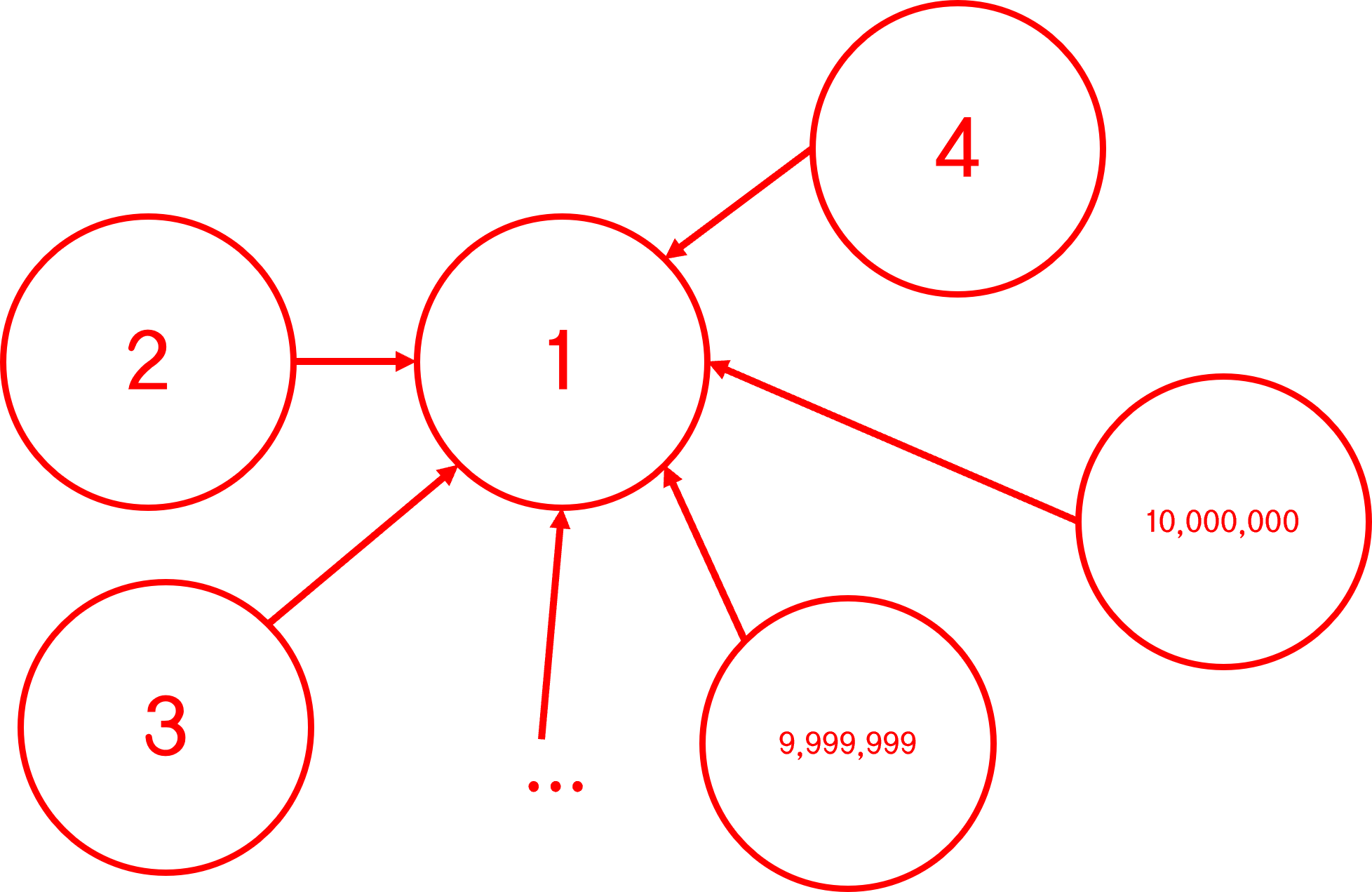

이러면 이제 Find() 호출로 시조 아래 다른 자식 노드들도 시조를 찾기가 엄청 쉬워졌다.
이렇게 줄이는 방법을 경로 압축이라고 부른다.
경로 압축을 적용하려면 코드를 어떻게 만들어야 할까?
int Find(int x) {
if (root[x] == x) return x;
return root[x] = Find(root[x]); // 대입 연산을 반환부로.
}
이렇게 대입 연산식 자체를 반환부에 넣어주면 된다.
그럼 대입이 일어나고, 그 값이 또 반환되어 넘어가 계속 반복된다.
그렇게 낮아진 트리의 높이로 시조를 찾는 과정이 훨씬 줄어들게 된다.
경로 압축으로 트리의 최대 높이가 O(α(N)) 역아커만 함수 수준으로 줄어들기 때문에,
시조를 찾는 과정이 사실상 O(1)처럼 동작하게 되기 때문에 꼭 챙겨가야 할 최적화 방법이다.
2. 랭크 기반 최적화 (Union by Rank / Union by Height)

이렇게 1부터 9까지 노드들이 있고,
1번을 루트로 둔 1-2-3-4-5 집합과 6, 7, 8, 9 집합으로 묶여 있는 상태라고 가정해보자.

여기서 2번 노드와 7번 노드를 연결하려고 하면, 2가지 상태가 가능하게 된다.
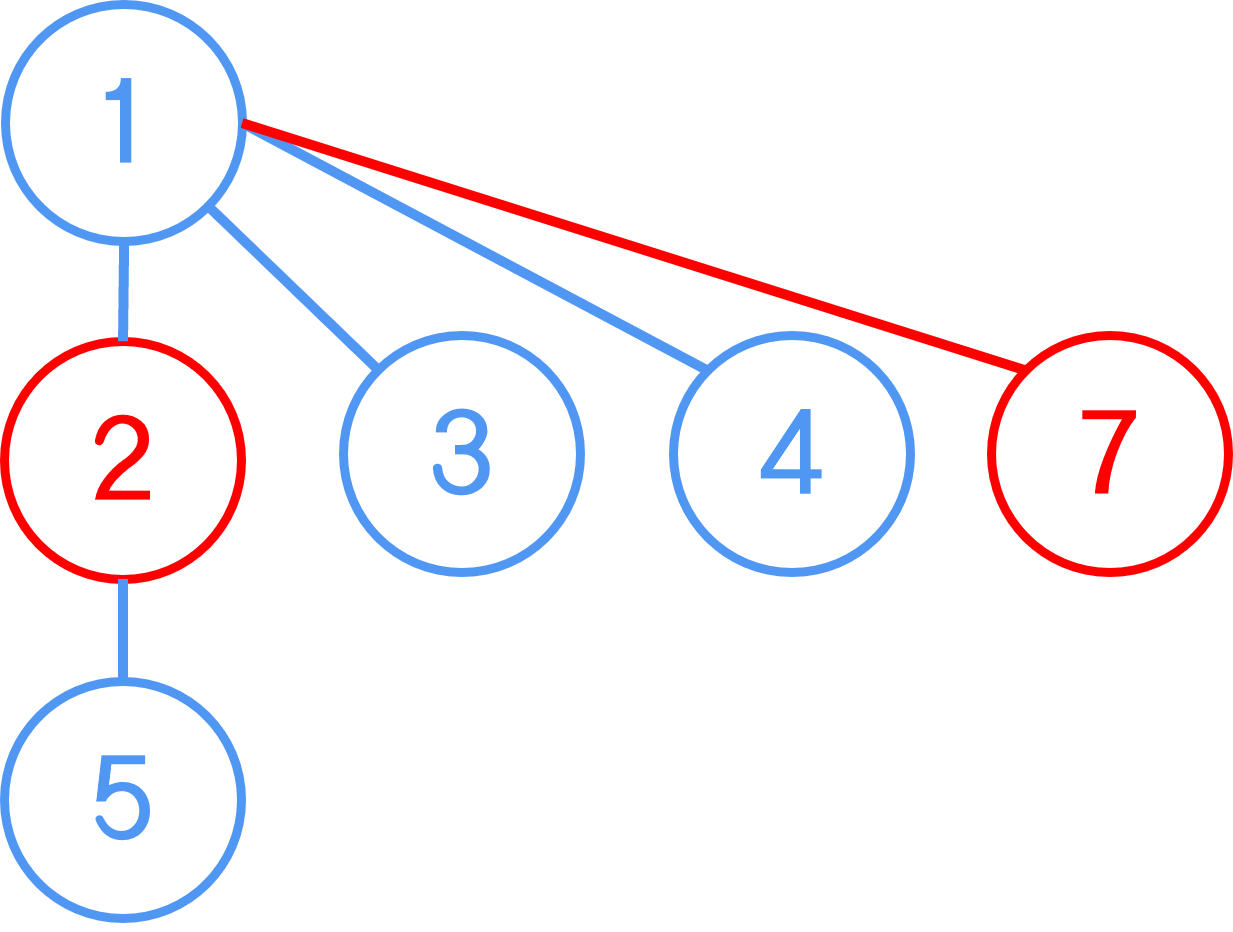
1. 이렇게 2번 노드가 속한 집합의 루트인 1번 노드에 7번 노드가 자식으로 연결되는 형태

2. 7번 노드 집합의 루트인 7번 노드에 2번 노드의 집합 루트인 1번 노드가 자식으로 연결되는 형태
그래서 뭐.
뭐가 다르냐하면,
경우에 따라 트리의 높이가 달라진다.
1번은 원래 높이였던 3에서 변하지 않은 반면,
2번의 경우엔 트리의 높이가 4로 확장됐다.
조금전 경로 압축 최적화를 다루면서 트리의 높이를 줄이는 것이 얼마나 중요한지 알아봤다.
트리의 높이가 높아지면 돼요~~? 안 돼요?
당연히 안 돼죠.
그러니깐, 트리의 높이도 낮은 놈이 굳이굳이 지가 루트가 돼보겠다고
더 높은 트리의 루트를 자식으로 두면 돼요~? 안 돼요?
안 되겠지.
그래서 트리의 높이(이걸 rank라고 부를 거임)를 저장해두고,
합집합 과정에서 두 노드의 시조가 다른 경우에 아무거나 마음대로 합치지 말고
높이가 더 낮은 집합의 시조가 높이가 더 높은 집합의 시조 자식으로 들어가는 게 합당하겠지.
그럼 이걸 코드에 적용하면?
void Union(int x, int y) {
int rootX = Find(x);
int rootY = Find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
root[rootY] = rootX;
}
else if (rank[rootX] < rank[rootY]) {
root[rootX] = rootY;
}
else {
root[rootY] = rootX;
rank[rootX]++; // 둘 다 높이가 같았으면 맘대로하고 높이 늘려주기.
}
}
}
부모를 저장하는 배열 root[] 외에도
트리의 높이를 저장하는 rank[]를 선언해서 관리해주면 된다.
3. 크기 기반 최적화 (Weighted Rule / Union by Size)
트리의 높이가 아니라 포함하고 있는 노드의 개수 즉, 전체 사이즈를 기준으로 보는 최적화 기법도 있는데
개인적인 의견으로 이건 굳이 쓸 필요 있나 싶다
지금까지 설명으로 트리의 높이가 시간에 얼마나 중요한 영향을 미치는 지는 잘 알게 됐을 거다.
그런데 높이 대신 그냥 개수라니?

이론 상으로도 높이 기반으로 최적화를 하는 게 더 효율적이다.
그래도 일단 알아보는 김에 얘도 소개해보겠다.
어렵진 않고, 말 그대로 높이를 저장하는 대신 트리의 크기를 저장하면 된다.
코드로 하면?
void Union(int x, int y) {
int rootX = Find(x);
int rootY = Find(y);
if (rootX != rootY) {
if (rank[rootX] < rank[rootY]) { // 크기를 비교.
root[rootX] = rootY;
size[rootY] += size[rootX]; // 상대 크기 흡수.
}
else {
root[rootY] = rootX;
size[rootX] += size[rootY];
}
}
}
합집합 연산 시에 크기를 비교해주고,
상대 트리 크기를 흡수하면 된다.
결론: 경로 압축만 써도 충분하다.
경로 압축 최적화 설명을 들어서 알겠지만,
웬만하면 트리 높이가 항상 2로 유지되는 방법이기 때문에 다른 최적화를 굳이 더 해줄 필요는 없다.
"아니, rank 기반으로 줄이잖어!!"
그렇지만, 경로 압축을 사용하면 rank 기반 최적화를 쓰는 의미가 사실상 거의 없어진다.
역아커만 함수 수준까지 트리의 높이가 낮아지기 때문에 굳이 더 최적화를 해주지 않아도 충분히 빠르다는 거다.
🪄 요약 & 마무리
자, 짧고 굵게 3줄 요약 들어간다.

1. 유니온 파인드란, 시조(루트/조상)를 비교해서 같은 집합에 속해있는지 알아내는 알고리듬이다.
// 시조 찾기.
int Find(int x) {
if (root[x] == x) return x;
return root[x] = Find(root[x]); // 경로 압축 최적화 적용.
}
// 합집합.
void Union(int x, int y) {
int rootX = Find(x); // x의 시조.
int rootY = Find(y); // y의 시조.
if (rootX != rootY)
root[rootY] = rootX; // 이제 y의 시조는 시조가 아니다.
}2. 유니온 파인드 알고리듬은 결국 시조를 찾는 함수(Find)와 합집합 하는 함수(Union)가 전부다.
3. 최적화 기법으로는 경로 압축(얘만 써도 문제없음), 랭크 기반 최적화가 있다.

'Algorithm > 이론' 카테고리의 다른 글
| [알고리듬/이론] 볼록 껍질 (Convex Hull) (0) | 2024.07.12 |
|---|